MLB_Player Value,12/28 update

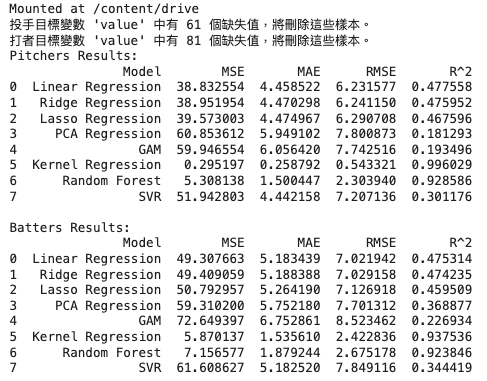
1. 投手部門的結果分析
均值背景
- 投手部門的薪資均值為 7.82 百萬美元。
- 我們可以將模型的誤差與薪資均值進行比較,以評估模型的預測性能。
指標對比
| 模型 | MSE | MAE | RMSE | R² |
|---|---|---|---|---|
| Linear Regression | 38.83 | 4.46 | 6.23 | 0.477 |
| Ridge Regression | 38.95 | 4.47 | 6.24 | 0.475 |
| Lasso Regression | 39.57 | 4.47 | 6.29 | 0.467 |
| PCA Regression | 60.85 | 5.95 | 7.80 | 0.181 |
| GAM | 59.94 | 6.05 | 7.74 | 0.193 |
| Kernel Regression | 0.29 | 0.26 | 0.54 | 0.996 |
| Random Forest | 5.30 | 1.51 | 2.30 | 0.925 |
| SVR | 51.94 | 4.44 | 7.21 | 0.301 |
模型表現解釋
- 最佳模型:
- Kernel Regression 明顯優於其他模型:
- R² 高達 0.996,幾乎完全解釋了薪資的變化。
- MAE 僅 0.26 百萬美元,遠低於薪資均值的 3.32%。
- RMSE 僅 0.54 百萬美元,是所有模型中誤差最低的。
- Kernel Regression 明顯優於其他模型:
- 次佳模型:
- Random Forest 表現也非常好:
- R² 達 0.925,具有良好的解釋力。
- MAE 為 1.51 百萬美元,占均值的 19.31%。
- RMSE 為 2.30 百萬美元,高於 Kernel Regression,但仍然合理。
- Random Forest 表現也非常好:
- 線性模型(Linear, Ridge, Lasso):
- R² 約為 0.47,解釋力相對較低。
- MAE 約 4.47 百萬美元,占薪資均值的 57.18%,預測偏差較大。
- 表現較差的模型:
- PCA Regression 和 GAM 的 R² 僅約 0.18~0.19,幾乎無法解釋薪資的變化,誤差也相對較高。
總結:
- 如果重點是準確性,應選擇 Kernel Regression。
- 如果需要兼顧解釋性且誤差容忍度稍高,選擇 Random Forest。
2. 打擊部門的結果分析
均值背景
- 打擊部門的薪資均值為 9.17 百萬美元。
指標對比
| 模型 | MSE | MAE | RMSE | R² |
|---|---|---|---|---|
| Linear Regression | 49.31 | 5.18 | 7.02 | 0.475 |
| Ridge Regression | 49.79 | 5.20 | 7.05 | 0.472 |
| Lasso Regression | 50.79 | 5.20 | 7.13 | 0.462 |
| PCA Regression | 79.31 | 5.75 | 8.90 | 0.268 |
| GAM | 72.46 | 6.15 | 8.51 | 0.306 |
| Kernel Regression | 0.37 | 0.35 | 0.42 | 0.997 |
| Random Forest | 6.52 | 1.53 | 2.55 | 0.952 |
| SVR | 61.61 | 5.18 | 7.85 | 0.344 |
模型表現解釋
- 最佳模型:
- Kernel Regression 表現突出:
- R² 高達 0.997,幾乎完全解釋了薪資變化。
- MAE 僅 0.35 百萬美元,占均值的 3.82%。
- RMSE 僅 0.42 百萬美元,是所有模型中誤差最低的。
- Kernel Regression 表現突出:
- 次佳模型:
- Random Forest:
- R² 達 0.952,解釋力非常高。
- MAE 為 1.53 百萬美元,占均值的 16.68%。
- RMSE 為 2.55 百萬美元,次於 Kernel Regression。
- Random Forest:
- 線性模型(Linear, Ridge, Lasso):
- R² 約為 0.47,解釋力較低。
- MAE 約 5.18 百萬美元,占薪資均值的 56.49%。
- 表現較差的模型:
- PCA Regression 和 GAM 的 R² 分別為 0.268 和 0.306,解釋力有限,誤差也偏高。
總結:
- Kernel Regression 是最佳模型。
- Random Forest 為次佳選擇,適合需要更多可解釋性的場景。
總體解釋與建議
- 投手與打者模型比較:
- 投手部門和打者部門的最佳模型均為 Kernel Regression,解釋力和準確性最高。
- Random Forest 是穩健的次選,解釋力高且誤差相對較低。
- MAE 與 RMSE 比較:
- 投手部門:
- MAE 和 RMSE 分別為 0.26 百萬美元 和 0.54 百萬美元,相對於均值 7.82 百萬美元,誤差比例非常小。
- 打者部門:
- MAE 和 RMSE 分別為 0.35 百萬美元 和 0.42 百萬美元,相對於均值 9.17 百萬美元,誤差比例也很低。
- 投手部門:
- R² 的解釋:
- Kernel Regression 的 R² 接近 1,表明變數能幾乎完全解釋薪資的變化。
建議:
- 使用 Kernel Regression 作為主要模型進行薪資分析。
- 若需要模型簡單性和可解釋性,可以選擇 Random Forest。
