VAR 的練習題

假設我們有三個變數:
- y1:銅價(以美元計)
- y2:黃金價格(以美元計)
- y3:台灣加權指數
這些數據是從2024年9月5日到2024年9月12日的,為了簡化分析,我們只考慮每個變數的前一天(滯後1期)的影響。
提供的數據:
| 日期 | 銅價 (美元) | 黃金價格 (美元) | 台灣加權指數 |
|---|---|---|---|
| 2024/9/5 | 4.07 | 2511 | 21188 |
| 2024/9/6 | 4.15 | 2493 | 21435 |
| 2024/9/9 | 4.85 | 2501 | 21144 |
| 2024/9/10 | 4.4 | 2512 | 21064 |
| 2024/9/11 | 4.08 | 2512 | 21031 |
| 2024/9/12 | 4.315 | 2551 | 21653 |
VAR(1)模型:
在 VAR(1) 模型中,每個變量的當前值是其自身以及其他變量前一天值的線性組合,例如:
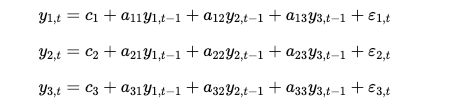
- a11,a12,a13:這些係數分別代表在銅價方程中,前一天的銅價、黃金價格和台灣加權指數對當天銅價的影響。
- a21,a22,a23:這些係數在黃金價格方程中描述了相同變量的影響。
- a31,a32,a3:這些係數在台灣加權指數方程中描述了相同變量的影響。
簡單估計 A1 矩陣的思路:
使用最簡單的方法來估計這些係數,我們可以查看每個變量從一天到另一天的變化,並嘗試估計這些變化與其他變量之間的關聯性。例如,如果我們觀察到當黃金價格上升時,銅價也上升,則可能在黃金價格方程中 a12a_{12}a12 係數為正。
模型的實際應用:
- 預測:一旦確定了模型參數,就可以用來預測未來價格和指數的變化。
- 政策制定:理解這些變量之間的相互作用可以幫助政策制定者和市場參與者做出更明智的決策。
讓我們進行一個簡化的計算示例,來展示如何手動估計向量自回歸(VAR)模型中的一些參數。我們將使用您提供的數據來進行試算,並僅考慮使用一個滯後期來估計模型。
假設我們有三個變數:
- y1:銅價(以美元計)
- y2:黃金價格(以美元計)
- y3:台灣加權指數
這些數據是從2024年9月5日到2024年9月12日的,為了簡化分析,我們只考慮每個變數的前一天(滯後1期)的影響。
提供的數據:
| 日期 | 銅價 (美元) | 黃金價格 (美元) | 台灣加權指數 |
|---|---|---|---|
| 2024/9/5 | 4.07 | 2511 | 21188 |
| 2024/9/6 | 4.15 | 2493 | 21435 |
| 2024/9/9 | 4.85 | 2501 | 21144 |
| 2024/9/10 | 4.4 | 2512 | 21064 |
| 2024/9/11 | 4.08 | 2512 | 21031 |
| 2024/9/12 | 4.315 | 2551 | 21653 |
簡化的估計方法:
為了估計 A1 矩陣的係數,我們將對數據進行簡單的差分,來獲得變化量,然後利用最小二乘法進行估計。這裡我們僅用最基本的手動計算方法進行示範,並不涉及所有的回歸細節。
假設我們只關注銅價對自身和黃金價格的影響,方程可以表示為:
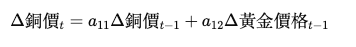
計算變化量 (差分):
- 銅價的變化量:Δ銅價
- 黃金價格的變化量:Δ黃金價格
例如:
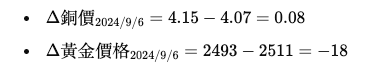
重複計算所有變化量。
建立簡化方程:
使用這些變化量,我們可以建立一個簡化的方程來估計 a11 和 a12,例如:
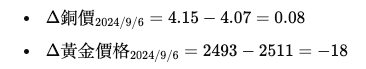
- 以此類推。
使用這些差分值填充到方程中,可以利用線性回歸方法估計 a11 和 a12 的值。
這是一個非常基礎的示範,不考慮控制變量、誤差項或統計檢驗。在實際應用中,這些計算需要使用統計軟體進行,以確保準確性和包含所有相關的統計檢驗。這裡的目的是展示基本的計算過程和思路。
如果把變數都設為當天的漲跌幅, 變數的內容全部都在 -1.0 至 1.0 之間,有意義嗎?
將變數設定為當天的漲跌幅(例如,使用百分比變化),並將數據範圍限制在 -1.0 至 1.0 之間,這是一種在金融和經濟時間序列分析中非常實用的方法。這種方法通常對於VAR模型和其他多變量時間序列模型來說非常有用,具體優缺點如下:
優點
- 消除量綱影響:
- 通過轉換為漲跌幅,不同變數即使原始單位不同(如銅價是美元/磅,指數是點數),也能在同一尺度上進行比較和分析。
- 增強模型的適應性:
- 使用漲跌幅作為變數,有助於捕捉變數間的動態關聯性,而不受絕對價值的影響,這對於金融市場分析尤為重要,因市場經常受到各種因素的影響,使價格波動。
- 方便模型預測:
- 預測未來的漲跌幅而非絕對價值,可以直接用於投資決策,例如股票交易策略的制定。
- 降低異常值的影響:
- 將變數限制在一定範圍內有助於減少極端值對模型的影響,提高模型的穩定性和預測準確度。
缺點
- 信息損失:
- 轉換為漲跌幅可能會丟失一些原始數據中的信息,特別是那些與價格水平相關的長期趨勢和季節性模式。
- 對於極端漲跌幅的處理:
- 如果市場出現非常劇烈的波動(如股市崩盤或快速上漲),漲跌幅可能會超出 -1.0 至 1.0 的範圍,需要特別處理這些情況以避免引入模型誤差。
- 數據前處理複雜性:
- 需要對數據進行額外的前處理,確保所有變數都被正確地轉換和標準化,這可能增加分析的複雜度。
- 可能忽視絕對價值的重要性:
- 在某些經濟和金融分析中,絕對價值本身就是重要的指標(如通貨膨脹分析中的消費者價格指數)。單純使用漲跌幅可能無法完全捕捉這些現象。
總結來說,將變數轉換為漲跌幅並保持在一定範圍內是一種有效的方法,特別是在需要分析多個不同單位或量綱的時間序列數據時。然而,這種方法是否適用還需根據具體的分析目的和數據特性來決定。
