向量自我迴歸模型(VAR)及其滯後值的邏輯

向量自我迴歸模型(VAR)是一種多變量的時間序列模型,它的特點是使用過去數據中的滯後值來解釋當前變量的變化。這裡的「滯後值」指的是變量在前一期或多期的歷史數據,而不是使用其他變量的當前值來解釋當前的數據。
滯後值的邏輯
滯後值是指在當前時間點之前的數據。對於時間序列數據,我們只能根據已經發生的事件或變量來預測或解釋當前的狀況。滯後值的核心邏輯在於:
- 時間依賴性:變量的未來值通常會受到其自身過去值的影響。例如,今天的經濟增長可能會與昨天的經濟增長有關。
- 變數之間的相互依賴性:VAR 模型認為多個變量之間存在動態關係,這些變量的滯後值可以用來解釋其他變量的當前值。例如,失業率的滯後值可能會對 GDP 成長率的當前值產生影響。
VAR 模型的正確描述
VAR 模型的核心是,每一個變量的當前值由其自身及其他所有變量的滯後值來解釋。換句話說,當前變量並不依賴於其他變量的當前值,而是依賴於過去的數據。因此,每個變數的當前值都是由其自身的歷史數據和其他變數的歷史數據共同決定的。
數學表示
對於一個有 ( n ) 個變數的 VAR(p) 模型,表示如下:
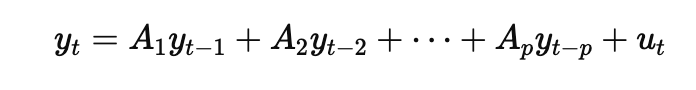
其中:
- yt是當前時間 ( t ) 的變量向量,包含 ( n ) 個變量(如 GDP 成長率、失業率等)。
- ( A1, A2,.....Ap ) 是係數矩陣,描述了每個變量的滯後值對當前值的影響。
- ( yt-1, yt-2, yt-p ) 是變量的滯後值,也就是變量在前 1 期、前 2 期到前 ( p ) 期的數值。
- ( ut ) 是誤差項,表示模型無法解釋的隨機波動。
簡單範例
假設我們有兩個變數:失業率(( y_1 ))和 GDP 成長率(( y_2 )),並使用一個滯後 1 期的 VAR(1) 模型。模型方程式如下:
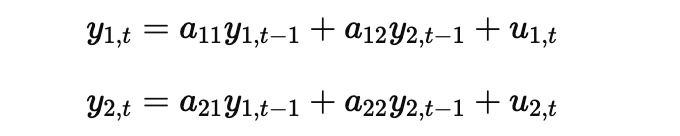
這個方程式表示:
- 當前時間 ( t ) 的失業率 ( y1,t ) 是由前一期的失業率 ( y1,t-1 ) 和前一期的 GDP 成長率 ( y_2,t-1 ) 共同決定的。
- 同樣,當前時間 ( t ) 的GDP 成長率 ( y_2,t ) 也是由前一期的失業率 ( y_1,t-1 ) 和前一期的 GDP 成長率 ( y_2,t-1 ) 來解釋的。
滯後值的邏輯補充
為什麼使用滯後值?在時間序列分析中,我們關注的是數據隨時間的變化,並且過去的數據通常會對未來產生影響。例如:
- 經濟增長通常會有一定的慣性,因此前幾期的經濟增長數據會對當前的經濟增長產生影響。
- 失業率也是如此,前幾期的失業狀況可能會影響企業的用工決策,從而對當前的失業率產生影響。
滯後值的使用使得 VAR 模型能夠捕捉變量之間的動態關係,而這種關係可能隨著時間的推移而變化。這正是滯後值在時間序列分析中非常關鍵的原因。
總結
- VAR 模型是一種多變量時間序列模型,它通過每個變量及其相關變量的滯後值來解釋當前的變量變化。
- 滯後值指的是變量在前幾個時間點的數據,它們是時間序列模型中用來預測未來的重要工具。
- 在 VAR 模型中,每個變量的當前值是由它自己和其他變量的滯後值來解釋,而不是由其他變量的當前值來解釋。這種結構能夠捕捉變量之間的動態依賴關係。
這種結構使得 VAR 模型非常適合分析經濟數據、金融市場等多變量系統的交互關係。
當然!為了讓這個例子更具體,我們可以把數據和計算過程以表格形式呈現,以便更清晰地理解 VAR 模型的應用。
數據表
以下是 2021 年至 2023 年的數據,並且我們將根據這些數據來預測 2024 年的經濟增長率和失業率。
| 年份 | 失業率 (( y_2 )) | 經濟增長率 (( y_1 )) |
|---|---|---|
| 2021 | 4.5% | 2.5% |
| 2022 | 4.3% | 2.8% |
| 2023 | 4.6% | 3.0% |
| 2024 | ? | ? |
VAR(1) 模型的方程
- 經濟增長率的方程:
[
y_{1,t} = a_{11} y_{1,t-1} + a_{12} y_{2,t-1} + u_{1,t}
] - 失業率的方程:
[
y_{2,t} = a_{21} y_{1,t-1} + a_{22} y_{2,t-1} + u_{2,t}
]
其中,係數已經預估如下:
- ( a_{11} = 0.6 )
- ( a_{12} = -0.3 )
- ( a_{21} = -0.5 )
- ( a_{22} = 0.7 )
計算過程表
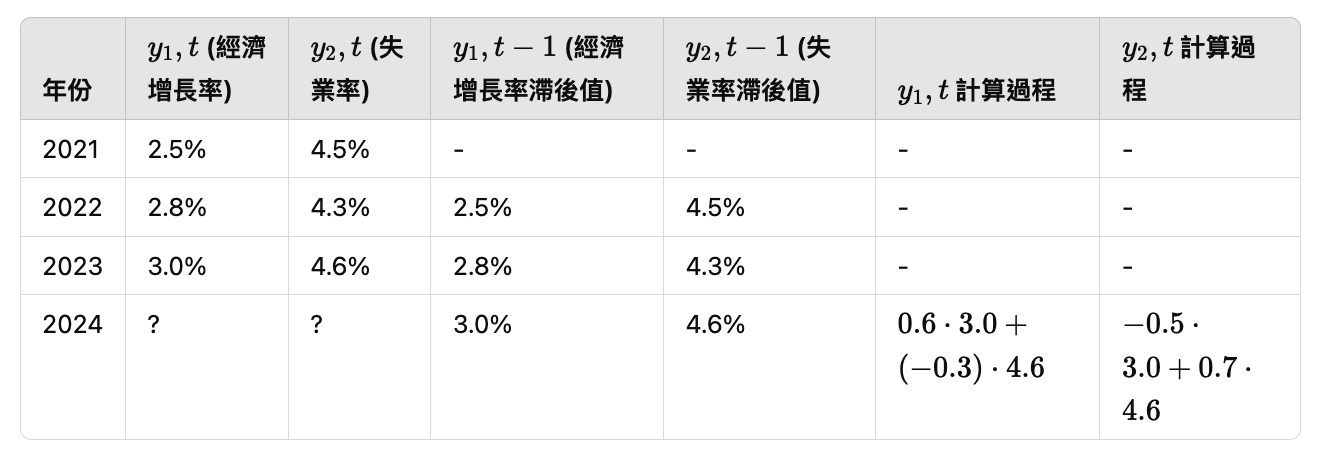
計算步驟

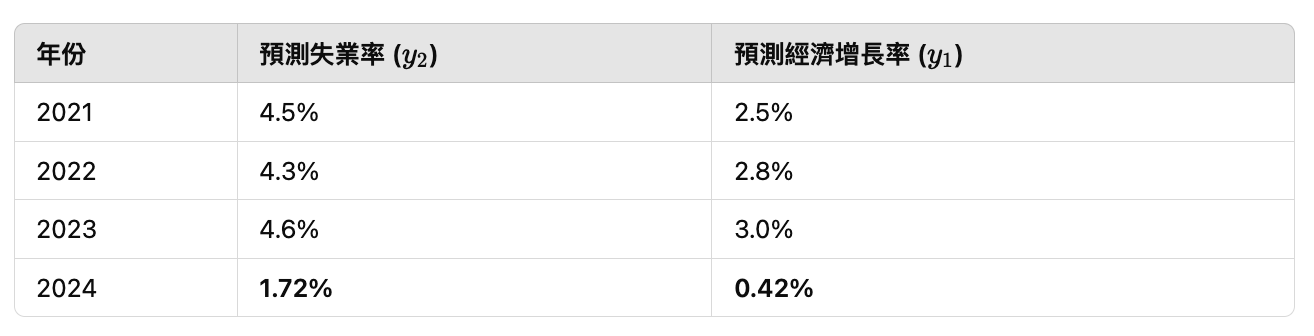
結果表
總結
- 我們使用 VAR(1) 模型,基於 2023 年的經濟增長率和失業率來預測 2024 年的數據。
- 模型預測 2024 年的經濟增長率為 0.42%,失業率為 1.72%。
- 這個例子展示了如何使用兩個變數的滯後值來進行預測,並且通過表格能夠更清楚地看到模型的運作方式。
這樣的表格展示可以幫助你直觀地理解 VAR 模型的計算過程,以及每個變數的滯後值對當前值的影響。
